[Statistics] 위치 추정 (평균, 중간값)

위치 추정?

데이터를 분석할 때, 데이터들이 표현하는 변수들을 수많은 값을 갖습니다. 데이터를 살펴보는 가장 기본적이고 기초적인 방법은 각 변수를 대표할 수 있는 값을 구하는 것 입니다. 이것을 '대푯값(typical value)'라고 합니다. 변수의 대부분의 값들이 어디쯤에 위치하는지를 알아보는 중심경향성을 나타내는 추정값입니다.

 

중요 개념정리

• 평균(mean)
• 가중평균(weighted mean) : 가중치를 곱한 값의 총합을 가중치의 총합으로 나눈 값
• 중간값(median)
• 가중 중간값(weighted median) : 데이터를 정렬한 후, 각 가중치 값을 더할 때, 총합의 중간이 위치하는 데이터 값
• 절사평균(trimmed median) : 정해진 개수의 극단값(extreame value)을 제외한 나머지 값들의 평균
• 로버스트하다(robust) : 극단값들에 민감하지 않다는 것을 의미한다. 저항성이 있다.
• 특이값(outlier) : 대부분의 값과 매우 다른 데이터 값 (극단값)

1. 위치 추정

1) 절사평균

절사평균은 평균을 변형한 것 중에 하나이다. 값들을 크기 순으로 정렬한 후, 양 끝에서 일정 개수(p)의 값을 삭제한 뒤 남은 값들을 가지고 구한 평균을 말한다.

절사평균은 극단값들에 영향을 많이 받지 않는 추정치입니다. 예를 들면, 신입사원을 채용하는 면접자리에서 5명의 면접관이 면접자들의 점수를 기입한다고 할때, 가장 낮은 점수와 가장 큰 점수는 버리고 평균을 구하는 것입니다. 이렇게하면 부정채용이나 채용비리 등을 막을 수 있습니다.

 

2) 가중평균

가중평균은 각 데이터 값에 가중치(w)를 곱한 값들의 총합을 다시 가중치의 총합으로 나눈 것입니다.

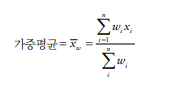
가중치를 사용하는 이유에는 2가지가 있습니다.

 

1. 어떤 값들이 본래 다른 값들에 비해 큰 변화량을 갖을 때. 이러한 관측값에 대해 더 작은 가중치를 줄 수 있다. 예를 들어 여러 개의 센서로부터 평균을 구한다고 할 때, 일부 센서의 정확도가 떨어진다면 해당 센서에서 나온 값들에 대해 가중치를 적용하는 것이 바람직하다고 할 수 있습니다.
2. 데이터를 수집할 때, 우리가 관심 있는 서로 다른 대조군에 대해서 항상 똑같은 수가 얻어지지는 않는다.

2. 중간값과 로버스트 추정

모든 관측치를 다 사용하는 평균과는 달리, 중간값은 정렬된 데이터의 가운데에 위치한 값들만으로 결정하는 추정치입니다. 데이터에 매우 민감한 평균과 달리 중간값이 많은 경우, 위치 추정에 더 유리합니다. 평균에 비해 Robust하다고 말할 수 있습니다.

 

1) 특이값

중간값은 결과를 왜곡할 수도 있는 특이값(극단값)들의 영향을 받지 않으므로 robust한 위치 추정방법이라고 합니다. 특이값은 한 데이터 집합에서 다른 값들의 정상적인 분포와 달리 극단적으로 멀리 떨어져 있는 값들을 말합니다. 특이값은 데이터 값 자체가 유효하지 않다거나 잘못되었다는 것이 아닙니다. 

 

절사평균에서는 가장 큰 5개 주의 인구와 가장 작은 5개 주의 인구를 제외하고 평균을 계산한다. trim_mean에서

0.1은 각 끝에서 10%를 제외하라는 뜻이다.

 

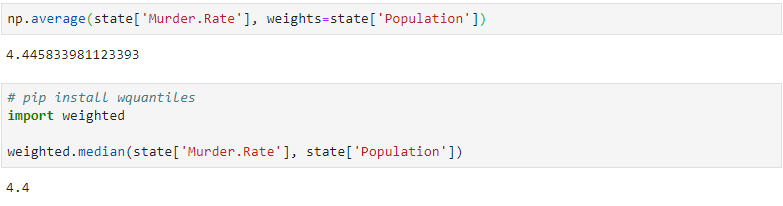
python에서 가중 중위수를 구하기 위해서는 wquantiles 패키지를 사용하면된다. pip install을 통해 wquantiles을 설치하고 불러와 사용한다.

 

정리

• 가장 기본적인 위치 추정 방법은 평균이다. 단, 극단값에 민감할 수 있다.
• 중간값, 절사평균과 같은 다른 방법들이 좀 더 로버스트하다.

 

'데이터 과학을 위한 통계 - 한빛미디어'를 공부하며 정리한 내용입니다.