[ML] 결정나무(Decision Tree)

이번 포스트에서는 머신러닝 모델 중 분류 모델의 기본이라고 할 수 있는 결정 나무 모델에 대해 알아보겠습니다. 구조도가 잎과 가지로 구성된 나무 같다고해서 결정 나무라고 불린다고 합니다.

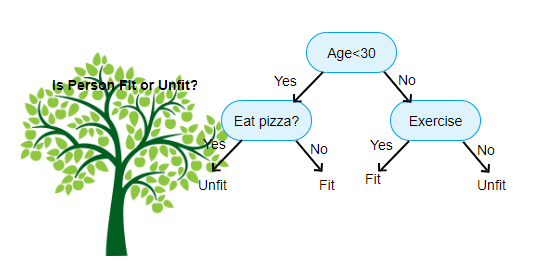
결정나무(Decision Tree)란?

설명변수들의 규칙, 관계, 패턴 등으로 관심 대상인 목표변수를 분류하는 나무 구조의 모델을 만들고, 설명변수의 값을 생성된 모델에 입력하여 목표변수를 분류 / 예측하는 지도학습 기법입니다. 간단히 말하자면 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 분류 규칙을 트리(Tree) 형태로 만드는 것입니다. 결정나무는 목표변수에 영향을 주는 설명변수를 탐색하고 해당 설명변수의 최적 분리기준을 제시합니다.

 

활용 예시

그렇다면 이 결정나무는 어떠한 상황에 활용되는지 살펴보겠습니다. 분류와 예측에따라 활용 방법이 조금 다릅니다.

 

■ 분류(classification)

- 분류 문제에서는 범주형 레이블을 예측합니다.

ex)

- 은행 입장에서 대출을 요청하는 고객의 특성에 따라 대출 위험성을 분석하여 대출 여부를 결정한다.

- 고객 프로파일 및 구매 패턴을 분석하여 새로운 제품 구매 여부를 판단한다.

- 환자 특성과 상태에 따라 특정 처방의 적절성 여부를 예측한다.

 

■ 회귀(regression)

- 회귀 문제에서는 목표변수의 평균값을 예측합니다.

ex)

- 다양한 신체 측정값을 기반으로 체질 비만도를 예측합니다.

- 주택가격에 영향을 주는 다양한 요인을 분석하여 주택 특성별 가격을 예측합니다.

- 고객 프로파일 및 구매 패턴에 따른 (특정) 제품 또는 매장의 매출액을 예측합니다.

 

분류와 회귀 둘 다 사용할 수 있지만 주로 분류 문제에서 더 자주 사용하곤합니다. 분류에서는 어떤 결정 요소에 따라 분류 값이 나왔는지 쉽게 이해할 수 있어 자주 활용됩니다. 반면, 회귀에서는 다른 모델에 비해 성능이 조금 떨어지기 때문에 자주 사용하지 않습니다.

 

 

트리 구조의 구조

위에 그림은 결정 트리의 구조에 대해 나타낸 것입니다. 각 용어에 대해 살펴보겠습니다.

 

- Decision Node(규칙 노드) : 트리의 규칙 조건이 되는 부분입니다. 데이터 셋에 다양한 피처들이 있고 이 피처들이 결합되어 규칙 조건을 만듭니다. 이 규칙 조건이 Decision Node입니다. 예를 들어 건강검진데이터를 사용한다고 가정했을 때, 남자인지 여자인지를 구분하는 노드라고 할 수 있습니다.

- Root Node : 루트 노드는 가장 상위에 있는 규칙노드입니다. 제일 첫번 째 규칙 조건에 해당합니다.

- Leaf Node(입사귀 노드) : 규칙 노드에 의해 결정된 클래스 값입니다. 위의 예시로 보자면 여자와 남자가 될 것입니다. 조건에 해당하여 구분된 값이라 할 수 있습니다. 트리 구조에서 가장 마지막에 있는 것들이 바로 Leaf Node입니다.

- Sub Tree : 서브 트리는 규칙 노드에 의해 분류된 입사귀 노드들을 포함한 한 그룹을 말합니다. 새로운 규칙 조건(규칙노드) 마다 서브 트리가 생성됩니다.

 

- Parent Node(부모 노드) : 부모 노드는 한 서브 트리 구조에서 Child Node(자식 노드)를 생성한 노드를 말합니다. 서브 트리에 따라서 부모 노드가 자식 노드가 될 수 있고 자식 노드가 부모 노드가 될 수 있는 구조입니다.

- Child Node(자식 노드) : 자식 노드는 한 Decision Node(결정 노드)에서 나온 또 다른 결정 노드입니다.

- Depth(깊이) : Depth는 트리 구조에서 말 그대로 깊이를 말합니다. 가장 위의 Root Node의 Depth는 0이고 밑으로 갈 수록 차례대로 1씩 증가합니다. 위의 그림에서는 Depth 2의 트리 구조라고 할 수 있습니다.

 

많은 규칙이 있을 수록 정확하게 분류 할 수 있을 것 같지만 규칙이 많아 질 수록 분류를 결정하는 방식 또한 복잡해집니다. 이는 과적합(Overfitting)이 될 가능성이 높아집니다. 즉, 트리의 깊이(depth)가 깊어질수록 결정 나무의 예측 성능이 떨어질 가능성이 높습니다.

 

그렇다면 높은 예측 정확도를 가진 결정 나무를 만들려면 어떻게 해야 할까요? 데이터를 분류할 때 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 결정 노드의 규칙이 정해져야합니다. 이를 위해선 트리를 최대한 균일한 데이터 세트를 구성할 수 있도록 분할(split) 해야합니다.

 

균일한 데이터 세트

그렇다면 균일한 데이터 세트라는 것은 무엇일까요? 위 그림을 통해 알아보도록 하겠습니다. 첫번 째로 보이는 집합은 하마, 독수리, 너구리, 강아지, 코브라로 되어있습니다. 이 경우에는 데이터가 다양하지만 균일하지는 않습니다. 반면 두번 째 집합은 너구리와 강아지로만 구성되어있습니다. 데이터가 다양하지는 않지만 균일합니다. 만약 위의 집합에서 아무거나 하나를 고르고 예측한다고 생각해봅시다. 두번 째 집합에서는 데이터가 균일하기 때문에 랜덤하게 하나를 뽑아도 너구리라고 예측할 확률이 높습니다. 하지만 첫번 째의 경우에는 혼잡도가 높기 때문에 데이터를 판단하기 쉽지 않습니다.

 

이와 같이 결정 노드는 정보 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙 조건을 생성합니다. 다시 말하자면, 정보 균일도가 높은 데이터 셋으로 나눠질 수 있도록 조건을 찾아 서브 데이터 셋을 생성하고, 생성한 자식 노드도 계속 반복적으로 정보 균일도가 높도록 조건을 찾습니다. 이 과정을 통해 데이터 값을 예측하게 됩니다. 이러한 정보의 균일도를 측정하는 분리기준에는 지니계수와 엔트로피가 있습니다.

 

결정 노드의 분리 기준

정보 균일도를 측정하는 분리 기준에는 지니 계수와 엔트로피 계수를 주로 사용합니다.

 

■ 지니 계수(Gini Index)

- 경제학에서 불평등 지수를 나타낼 때 주로 사용합니다.

- 불순도 측정 계수로 부모 노드의 지니 지수를 가장 많이 감소시키는 설명변수와 분리 값을 기준으로 자식노드를 형성합니다.

- 지니 계수가 낮을수록 데이터의 균일도는 높습니다. 따라서 지니 계수가 낮은 속성을 기준으로 분할합니다.

 

■ 엔트로피 계수(Entrophy Index)

- 엔트로피란 주어진 데이터 집합의 혼잡도를 의미합니다. 서로 다른 값이 섞여있으면 엔트로피가 높고, 같은 값들이 많으면 낮습니다.

- 혼잡도 측정지수로 부모 노드의 엔트로피 지수를 가장 많이 감소시키는 설명변수와 분리 값을 기준으로 자식 노드를 형성합니다.

- 분리에 필요한 기대 정보량으로 엔트로피가 낮을수록 균일도는 높습니다.

- 정보 이득 지수는 1에서 엔트로피 계수를 뺀 값입니다. 1-엔트로피 계수

- 결정 트리는 정보 이득 지수로 분할 기준을 결정하고 정보 이득이 높은 속성 기준으로 분할합니다.

 

결정 나무의 알고리즘

파이썬 머신러닝 완벽 가이드(위키북스)의 그림을 가져왔습니다.

결정 트리의 알고리즘은 데이터 세트를 분할하는 데 가장 좋은 조건(엔트로피 계수나 지니 계수에 의한)을 찾아 자식 노드를 거쳐 계속적으로 반복 분할한 뒤, 데이터가 모두 특정 분류에 속하게 되면 분할을 멈추고 분류를 결정합니다.

 

결정 나무의 특징

결정 나무의 가장 큰 장점은 데이터의 균일도를 기반으로하기 때문에 모델의 알고리즘이 쉽고 직관적이라는 점입니다. 또한 정보 균일도만 신경 쓰면 되므로 각 피처의 스케일링과 정규화 같은 전처리 작업이 필요없습니다. 하지만 단점은 과적합으로 인한 정확도가 떨어진다는 점입니다. 많은 서브 트리와 조건들이 생성되다 보면 데이터의 변수와 클래스가 많을 수록 트리의 깊이가 깊어지고 복잡해지 때문입니다. 따라서 결정 나무의 크기를 사전에 제한하는 방법으로 성능을 향상시킬 수 있습니다.

 

 

이상으로 결정 나무의 개념과 특징에 대해서 알아보았습니다. 다음 포스트에서는 결정 나무 모델을 사용한 실습을 진행해보도록 하겠습니다. 부족한 글 읽어주셔서 감사합니다.

 

 

※ 참고자료
- 파이썬 머신러닝 완벽 가이드, 권철민, 위키북스